Fun with the Mercator Projection
September 2010
On my brother’s wall is a map of Earth with the South Pole at the top. It uses an equal-area projection to show the true relative sizes of, say, Africa and Greenland. It aims to make a point about the more common North-up, Mercator projection. Mercator projection maps enlarge areas near the poles so that shapes are preserved. I like the sentiment but I think switching to an equal area projection and printing it upside-down is a little unimaginative. So I created this:
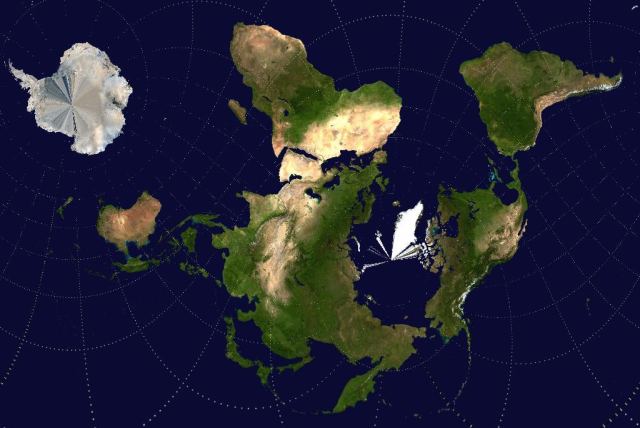
This is a map of Earth created using a Mercator projection, but with the magnified poles moved to the Atlantic and Pacific oceans. I created it using the Blue Marble map from Wikipedia. The dashed lines are the conventional latitude and longitude lines. You get a much better feel for the shape of Antarctica than normal Mercator maps give you, instead exaggerating Kamchatka.
Because, the Mercator projection doesn’t need to make Africa small and Greenland big. It can do anything you want it to. So for example, here is my little rebellion against Mercator’s underplaying of Africa’s troubles: a Mercator map in which the continent is infinite in area:

I’ve cropped the image here. In principle a Mercator projection can be continued infinitely in the vertical direction, and in this case the ‘north’ pole is in Africa, so the map would be Africa all the way up. The level of detail would, source image notwithstanding, get bigger and bigger until eventually sub-atomic particles started to appear. Theoretically, you could exploit this to produce a map where Britain opened out as Africa has at the top, and extend the map up to include a road map of England, including a large-scale street map of Manchester, eventually opening out to provide a floor-plan of one particular building, then room, and eventually the layout of one table. This, however, seems like it would be very difficult so I haven’t bothered.
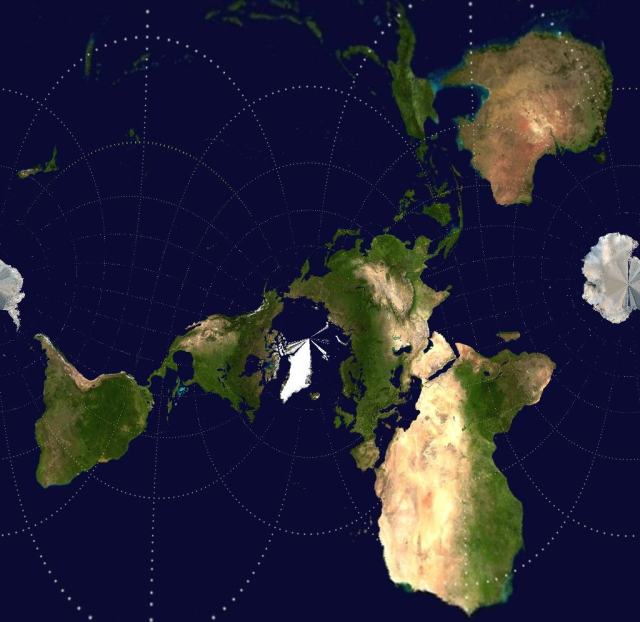
Here’s another Mercator map, this time with the poles near Australia and Africa again:
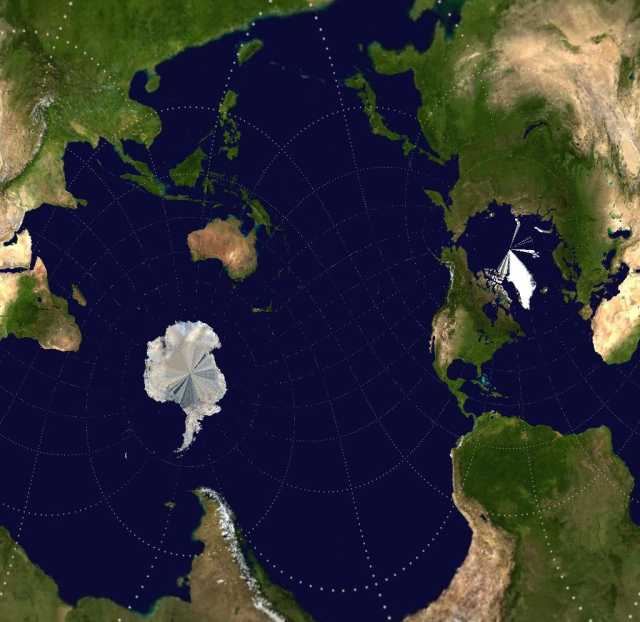
And here’s one with poles in Asia and South America, creating a world with one central ocean:
If you want to generate your own maps, use my Mercator Rotator toy.